الگوریتم مرتب سازی شانه ای (Comb Sort)

دوشنبه ۲۷ آبان ۱۳۹۸
بازدید ۱,۹۴۶ نفر
AmRo
(10 امتیاز از 2 رای)
Loading...

تصویر comb-sort-algorithm_7350 الگوریتم مرتب سازی شانه ای (Comb Sort)

الگوریتم مرتب سازی شانه ای (Comb Sort)

ایده اصلی مرتب سازی حبابی و مرتب سازی شانه ای یکی است. به عبارت دیگر می توان گفت که الگوریتم مرتب سازی شانه ای (Comb Sort)، بهبود یافته الگوریتم Bubble Sort است. در روش مرتب سازی حبابی، در هر مرحله هر مقدار با مقدار بعدی مقایسه می شود و میزان شکاف (Gap) همیشه 1 است. اما در مرتب سازی شانه ای، موارد در یک شکاف خاص طبقه بندی می شوند و بعد از اتمام هر مرحله، اندازه شکاف کاهش می یابد تا به 1 برسد. ضریب کاهش شکاف 1.3 است. یعنی پس از اتمام هر مرحله شکاف بر 1.3 تقسیم می شود.

تصویر comb-sort-algorithm_4350_1 الگوریتم مرتب سازی شانه ای (Comb Sort)

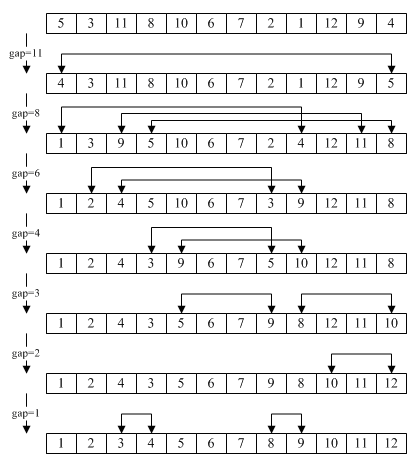
پیاده سازی الگوریتم Comb Sort

پیاده سازی الگوریتم مرتب سازی شانه ای با استفاده از زبان برنامه نویسی سی پلاس پلاس :

// C++ implementation of Comb Sort
#include<bits/stdc++.h>
using namespace std;
// To find gap between elements
int getNextGap(int gap)
{
    // Shrink gap by Shrink factor
    gap = (gap*10)/13;
    if (gap < 1)
        return 1;
    return gap;
}
// Function to sort a[0..n-1] using Comb Sort
void combSort(int a[], int n)
{
    // Initialize gap
    int gap = n;
    // Initialize swapped as true to make sure that
    // loop runs
    bool swapped = true;
    // Keep running while gap is more than 1 and last
    // iteration caused a swap
    while (gap != 1 || swapped == true)
    {
        // Find next gap
        gap = getNextGap(gap);
        // Initialize swapped as false so that we can
        // check if swap happened or not
        swapped = false;

        // Compare all elements with current gap
        for (int i=0; i<n-gap; i++)
        {
            if (a[i] > a[i+gap])
            {
                swap(a[i], a[i+gap]);
                swapped = true;
            }
        }
    }
}
// Driver program
int main()
{
    int a[] = {8, 4, 1, 56, 3, -44, 23, -6, 28, 0};
    int n = sizeof(a)/sizeof(a[0]);
    combSort(a, n);
    printf("Sorted array: \n");
    for (int i=0; i<n; i++)
        printf("%d ", a[i]);
    return 0;
}

// C++ implementation of Comb Sort

#include<bits/stdc++.h>

using namespace std;

// To find gap between elements

int getNextGap(int gap)

{

// Shrink gap by Shrink factor

gap = (gap*10)/13;

if (gap < 1)

return 1;

return gap;

}

// Function to sort a[0..n-1] using Comb Sort

void combSort(int a[], int n)

{

// Initialize gap

int gap = n;

// Initialize swapped as true to make sure that

// loop runs

bool swapped = true;

// Keep running while gap is more than 1 and last

// iteration caused a swap

while (gap != 1 || swapped == true)

{

// Find next gap

gap = getNextGap(gap);

// Initialize swapped as false so that we can

// check if swap happened or not

swapped = false;

// Compare all elements with current gap

for (int i=0; i<n-gap; i++)

{

if (a[i] > a[i+gap])

{

swap(a[i], a[i+gap]);

swapped = true;

}

// Driver program

int main()

{

int a[] = {8, 4, 1, 56, 3, -44, 23, -6, 28, 0};

int n = sizeof(a)/sizeof(a[0]);

combSort(a, n);

printf("Sorted array: \n");

for (int i=0; i<n; i++)

printf("%d ", a[i]);

return 0;

}

امتحان کنید

خروجی:

Sorted array:
-44 -6 0 1 3 4 8 23 28 56

1 2	Sorted array: -44 -6 0 1 3 4 8 23 28 56

شبیه سازی

آرایه زیر را در نظر بگیرید (مقدار اولیه شکاف 10 است):

8, 4, 1, 56, 3, -44, 23, -6, 28, 0
مقدار جدید شکاف: 10/1.3 = 7
8 4 1 56 3 -44 23 -6 28 0
-6 4 1 56 3 -44 23  8 28 0
-6 4 0 56 3 -44 23  8 28 1
مقدار جدید شکاف: 7/1.3 = 5
-44 4 0 56 3 -6 23 8 28 1
-44 4 0 28 3 -6 23 8 56 1
-44 4 0 28 1 -6 23 8 56 3
مقدار جدید شکاف: 5/1.3 = 3
-44 1  0 28 4 -6 23 8 56 3
-44 1 -6 28 4  0 23 8 56 3
-44 1 -6 23 4  0 28 8 56 3
-44 1 -6 23 4  0  3 8 56 28
مقدار جدید شکاف: 3/1.3 = 2
-44 1 -6 0 4 23 3 8 56 28
-44 1 -6 0 3 23 4 8 56 28
-44 1 -6 0 3 8 4 23 56 28
مقدار جدید شکاف: 2/1.3 = 1
-44 -6 1 0 3 8 4 23 56 28
-44 -6 0 1 3 8 4 23 56 28
-44 -6 0 1 3 4 8 23 56 28
-44 -6 0 1 3 4 8 23 28 56