الگوریتم مرتب سازی لانه کبوتری (Pigeonhole Sort)

چهارشنبه ۲۹ آبان ۱۳۹۸
بازدید ۲,۲۲۳ نفر
آرتین
(15 امتیاز از 3 رای)
Loading...

تصویر pigeonhole-sort-algorithm_7379 الگوریتم مرتب سازی لانه کبوتری (Pigeonhole Sort)

الگوریتم مرتب سازی لانه کبوتری (Pigeonhole Sort)

الگوریتم مرتب سازی لانه کبوتری (Pigeonhole Sort) یک الگوریتم مرتب سازی غیر مقایسه ای است که برای برای لیست هایی که عناصر آن ها مقادیر عددی هستند و همچنن لیست هایی ، اعداد ممکن برای مقادیر کلید نیز تقریبا مشابه اند، مناسب است. این الگوریتم از درجه O(n + Range) است که در آن n تعداد عناصر آرایه ورودی و Range تعداد مقادیر ممکن در آرایه است.

نحوه کار الگوریتم Pigeonhole Sort

ابتدا مقادیر کمینه و بیشینه را در بین عناصر آرایه پیدا می کنیم. سپس مقدار کمینه را min و مقدار بیشینه را max نامگذاری می کنیم.
مقدار Range را به شکل max-min+1 بدست می آوریم.
یک آرایه به اندازه Range با نام “pigeonholes” و مقدار اولیه خالی ایجاد می کنیم.
هر یک از عناصر را بررسی و در لانه کبوتری خودش قرار می دهیم. عنصر موجود در اندیس arr[i]، در لانه ای که دارای اندیس arr[i] – min است، قرار می گیرد.
حلقه را در سراسر آرایه “pigeonholes” اجرا می کنیم و عناصر لانه هایی که خالی نیستند را در آرایه اصلی قرار می دهیم.

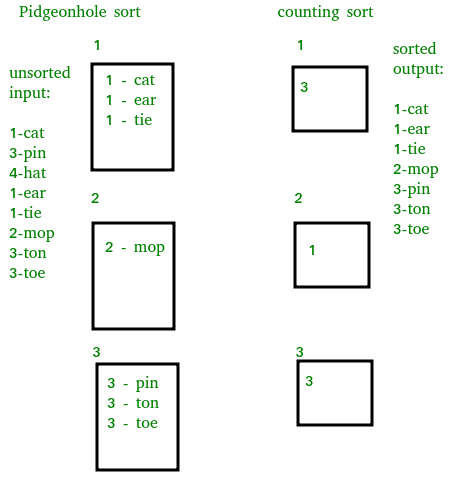
الگوریتم Pigeonhole Sort و Counting Sort

تفاوت اصلی موجود بین این دو الگوریتم مرتب سازی در این است که در مرتب سازی لانه کبوتری، عناصر دوبار جا به جا می شوند. بار اول به آرایه pigeonhole و بار دوم به آرایه اصلی.

تصویر pigeonhole-sort-algorithm_7379 الگوریتم مرتب سازی لانه کبوتری (Pigeonhole Sort)

پیاده سازی الگوریتم مرتب سازی لانه کبوتری

نحوه پیاده سازی الگوریتم مرتب سازی لانه کبوتری با استفاده از زبان برنامه نویسی سی پلاس پلاس:

/* C program to implement Pigeonhole Sort */
#include <bits/stdc++.h>
using namespace std;
/* Sorts the array using pigeonhole algorithm */
void pigeonholeSort(int arr[], int n)
{
    // Find minimum and maximum values in arr[]
    int min = arr[0], max = arr[0];
    for (int i = 1; i < n; i++)
    {
        if (arr[i] < min)
            min = arr[i];
        if (arr[i] > max)
            max = arr[i];
    }
    int range = max - min + 1; // Find range
    // Create an array of vectors. Size of array
    // range. Each vector represents a hole that
    // is going to contain matching elements.
    vector<int> holes[range];
    // Traverse through input array and put every
    // element in its respective hole
    for (int i = 0; i < n; i++)
        holes[arr[i]-min].push_back(arr[i]);
    // Traverse through all holes one by one. For
    // every hole, take its elements and put in
    // array.
    int index = 0;  // index in sorted array
    for (int i = 0; i < range; i++)
    {
       vector<int>::iterator it;
       for (it = holes[i].begin(); it != holes[i].end(); ++it)
            arr[index++]  = *it;
    }
}
// Driver program to test the above function
int main()
{
    int arr[] = {8, 3, 2, 7, 4, 6, 8};
    int n = sizeof(arr)/sizeof(arr[0]);
    pigeonholeSort(arr, n);
    printf("Sorted order is : ");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    return 0;
}

/* C program to implement Pigeonhole Sort */

#include <bits/stdc++.h>

using namespace std;

/* Sorts the array using pigeonhole algorithm */

void pigeonholeSort(int arr[], int n)

{

// Find minimum and maximum values in arr[]

int min = arr[0], max = arr[0];

for (int i = 1; i < n; i++)

{

if (arr[i] < min)

min = arr[i];

if (arr[i] > max)

max = arr[i];

}

int range = max - min + 1; // Find range

// Create an array of vectors. Size of array

// range. Each vector represents a hole that

// is going to contain matching elements.

vector<int> holes[range];

// Traverse through input array and put every

// element in its respective hole

for (int i = 0; i < n; i++)

holes[arr[i]-min].push_back(arr[i]);

// Traverse through all holes one by one. For

// every hole, take its elements and put in

// array.

int index = 0; // index in sorted array

for (int i = 0; i < range; i++)

{

vector<int>::iterator it;

for (it = holes[i].begin(); it != holes[i].end(); ++it)

arr[index++] = *it;

}

// Driver program to test the above function

int main()

{

int arr[] = {8, 3, 2, 7, 4, 6, 8};

int n = sizeof(arr)/sizeof(arr[0]);

pigeonholeSort(arr, n);

printf("Sorted order is : ");

for (int i = 0; i < n; i++)

printf("%d ", arr[i]);

return 0;

}

امتحان کنید

خروجی:

Sorted order is : 2 3 4 6 7 8 8

1	Sorted order is : 2 3 4 6 7 8 8

از آنجا که موارد مورد نیاز برای الگوریتم مرتب سازی لانه کبوتری به ندرت تامین می شود، استفاده از آن بسیار محدود است. در آرایه هایی که در آن مقدار Range بزرگتر از مقدار n است، الگوریتم Bucket Sort کارایی بهتری دارد.

نکات