الگوریتم مرتب سازی دایره ای (Cycle Sort)

شنبه ۲ آذر ۱۳۹۸
بازدید ۱,۶۸۳ نفر
سعید سیفی زاده
(10 امتیاز از 2 رای)
Loading...

تصویر cycle-sort-algorithm_7397 الگوریتم مرتب سازی دایره ای (Cycle Sort)

الگوریتم مرتب سازی دایره ای (Cycle Sort)

الگوریتم مرتب سازی دایره ای (Cycle Sort) یک الگوریتم مرتب سازی ناپایدار، درجا و مبتنی بر مقایسه است که از نظر تعداد دفعات نوشتن بر روی حافظه بهینه است (اگر عنصری در جای درست قرار داشته باشد، مقدار حافظه ای نوشته شده برای آن صفر خواهد بود). زمانی که محدودیت نوشتن بر روی حافظه داریم، استفاده از این الگوریتم می تواند بسیار مناسب باشد.

تصویر cycle-sort-algorithm_7397_1 الگوریتم مرتب سازی دایره ای (Cycle Sort)

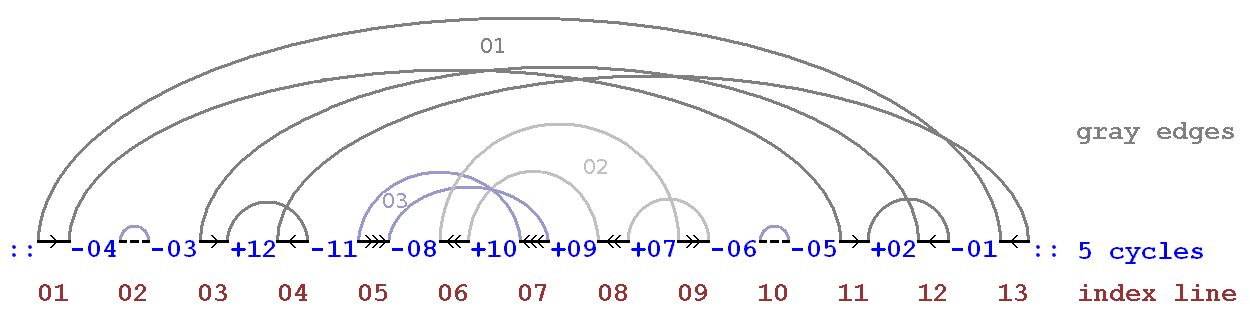
شبه کد الگوریتم Cycle Sort

arr[] = {10, 5, 2, 3}
 index =  0   1   2   3
cycle_start = 0
item = 10 = arr[0]
Find position where we put the item 
pos = cycle_start
while (arr[i] < item) 
    pos++;
We put 10 at arr[3] and change item to
old value of arr[3].
arr[] = {10, 5, 2, 10}
item = 3
Again rotate rest cycle that start with index '0'
Find position where we put the item = 3
we swap item with element at arr[1] now
arr[] = {10, 3, 2, 10}
item = 5
Again rotate rest cycle that start with index '0' and item = 5
we swap item with element at arr[2].
arr[] = {10, 3, 5, 10 }
item = 2
Again rotate rest cycle that start with index '0' and item = 2
arr[] = {2, 3,  5, 10}  
Above is one iteration for cycle_stat = 0.
Repeat above steps for cycle_start = 1, 2, ..n-2

arr[] = {10, 5, 2, 3}

index = 0 1 2 3

cycle_start = 0

item = 10 = arr[0]

Find position where we put the item

pos = cycle_start

while (arr[i] < item)

pos++;

We put 10 at arr[3] and change item to

old value of arr[3].

arr[] = {10, 5, 2, 10}

item = 3

Again rotate rest cycle that start with index '0'

Find position where we put the item = 3

we swap item with element at arr[1] now

arr[] = {10, 3, 2, 10}

item = 5

Again rotate rest cycle that start with index '0' and item = 5

we swap item with element at arr[2].

arr[] = {10, 3, 5, 10 }

item = 2

Again rotate rest cycle that start with index '0' and item = 2

arr[] = {2, 3, 5, 10}

Above is one iteration for cycle_stat = 0.

Repeat above steps for cycle_start = 1, 2, ..n-2

پیاده سازی الگوریتم Cycle Sort

نحوه پیاده سازی الگوریتم مرتب سازی دایره ای با استفاده از زبان برنامه نویسی C++:

// C++ program to implement cycle sort
#include <iostream>
using namespace std;
// Function sort the array using Cycle sort
void cycleSort(int arr[], int n)
{
    // count number of memory writes
    int writes = 0;
    // traverse array elements and put it to on
    // the right place
    for (int cycle_start = 0; cycle_start <= n - 2; cycle_start++) {
        // initialize item as starting point
        int item = arr[cycle_start];
        // Find position where we put the item. We basically
        // count all smaller elements on right side of item.
        int pos = cycle_start;
        for (int i = cycle_start + 1; i < n; i++)
            if (arr[i] < item)
                pos++;
        // If item is already in correct position
        if (pos == cycle_start)
            continue;
        // ignore all duplicate  elements
        while (item == arr[pos])
            pos += 1;
        // put the item to it's right position
        if (pos != cycle_start) {
            swap(item, arr[pos]);
            writes++;
        }
        // Rotate rest of the cycle
        while (pos != cycle_start) {
            pos = cycle_start;
            // Find position where we put the element
            for (int i = cycle_start + 1; i < n; i++)
                if (arr[i] < item)
                    pos += 1;
            // ignore all duplicate  elements
            while (item == arr[pos])
                pos += 1;
            // put the item to it's right position
            if (item != arr[pos]) {
                swap(item, arr[pos]);
                writes++;
            }
        }
    }
     // Number of memory writes or swaps
    // cout << writes << endl ;
}
// Driver program to test above function
int main()
{
    int arr[] = { 1, 8, 3, 9, 10, 10, 2, 4 };
    int n = sizeof(arr) / sizeof(arr[0]);
    cycleSort(arr, n);
    cout << "After sort : " << endl;
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
    return 0;
}