
الگوریتم مرتب سازی شل (Shell Sort)
الگوریتم مرتب سازی شل (Shell Sort) نسخه تغییر یافته الگوریتم مرتب سازی درجی (Insertion Sort) است. در مرتب سازی درجی ما عناصر را فقط یک خانه به جلو حرکت دهیم. همین موضوع باعث می شود تا برای انتقال یک عنصر به موقعیت خیلی جلوتر، تعداد حرکات افزایش یابد. در الگوریتم مرتب سازی شل امکان مبادله عناصر دور هم فراهم شده است.
الگوریتم مرتب سازی شل برای رفع ایرادات زیر که در مرتب سازی درجی وجود دارد، ایجاد شده است:
- کارایی مرتب سازی درجی زمانی خوب است که آرایه تقریبا مرتب باشد.
- بازده کمی دارد، چون در هر زمان فقط به اندازه یک موقعیت مقادیر را جا به جا می می کند.
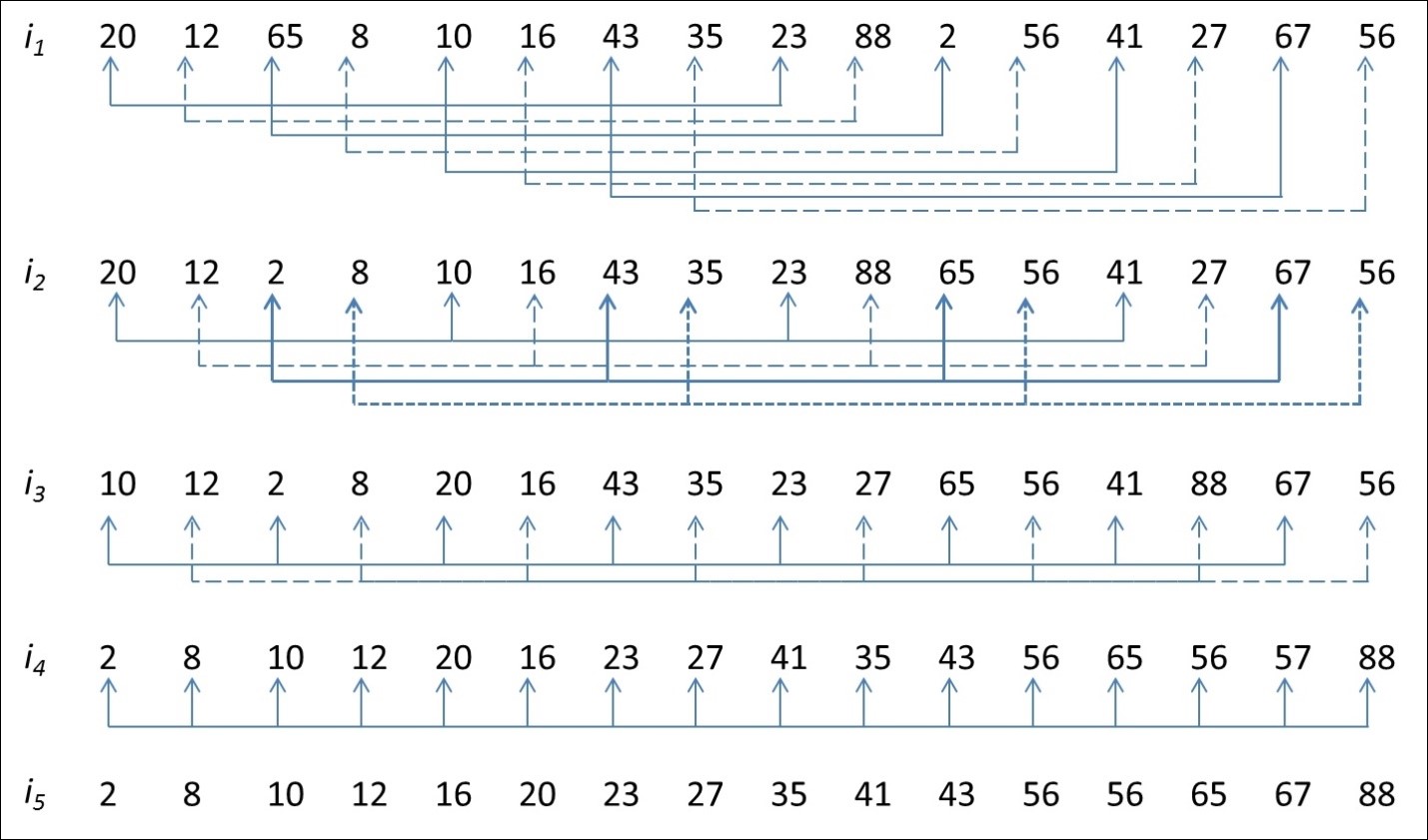
پیاده سازی الگوریتم Shell Sort
در زیر می توانید نحوه پیاده سازی الگوریتم Shell Sort با استفاده از زبان برنامه نویسی سی پلاس پلاس را مشاهده کنید:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | // C++ implementation of Shell Sort #include <iostream> using namespace std; /* function to sort arr using shellSort */ int shellSort(int arr[], int n) { // Start with a big gap, then reduce the gap for (int gap = n/2; gap > 0; gap /= 2) { // Do a gapped insertion sort for this gap size. // The first gap elements a[0..gap-1] are already in gapped order // keep adding one more element until the entire array is // gap sorted for (int i = gap; i < n; i += 1) { // add a[i] to the elements that have been gap sorted // save a[i] in temp and make a hole at position i int temp = arr[i]; // shift earlier gap-sorted elements up until the correct // location for a[i] is found int j; for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) arr[j] = arr[j - gap]; // put temp (the original a[i]) in its correct location arr[j] = temp; } } return 0; } void printArray(int arr[], int n) { for (int i=0; i<n; i++) cout << arr[i] << " "; } int main() { int arr[] = {12, 34, 54, 2, 3}, i; int n = sizeof(arr)/sizeof(arr[0]); cout << "Array before sorting: n"; printArray(arr, n); shellSort(arr, n); cout << "nArray after sorting: n"; printArray(arr, n); return 0; } |
خروجی:
1 2 3 4 | Array before sorting: 12 34 54 2 3 Array after sorting: 2 3 12 34 54 |
نکات
- پیچیدگی زمانی در بهترین حالت برابر است با O(n log2n).
- پیچیدگی زمانی در حالت متوسط برابر است با O(n2).
- پیچیدگی زمانی در بدترین حالت برابر است با O(n log2).
- پیچیدگی فضایی برابر است با O(1).





























سلام، خیلی عالی، ممنون بابت زحمتتون، فقط راجع به پیچیدگی زمانی فک کنم ایرادایی وجود داره، مثلا بهترین حالت o(n) هستش فک کنم. خط for (int i = gap; i < n; i += 1) هم باید به صورت زیر اصلاح بشه: for (int i = gap; i < n; i += gap)